
It's not that easy...
Of course, there are a couple of more advanced concepts that need to be discussed along with the basics.If you've read my Watercooling 101 primer, you're already familiar with part of what we're going to cover here. But, that was nothing more than one or two small paragraphs, hardly covering what we need to truly understand these concepts in a working waterblock.
We've redefined what a waterblock actually does and applied some good basic rules, but there's a lot more behind why they work. And I'd assume that's why we're all here, right? We know they do work – but why?
In order to truly get why ridges and nozzle choices and space layout are all so finely tuned, we have to understand some physics. Specifically, we need to cover the ideas of laminar and turbulent flow. And we need to get down to the bottom of the biggest enemy to cooling – the boundary layer.
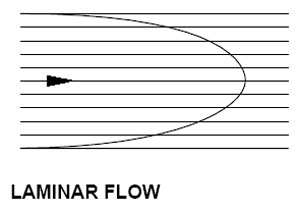
Laminar Flow is done in smooth layers,
with the outside being the slowest.
Laminar Flow
Laminar (or "smooth") flow is the physical property of a liquid to act much like an onion. Imagine a column of water to be like a green onion or leek – with cylindrical layers. The outermost layer is the slowest, while the innermost layers are the fastest. "But this is just water," I hear some of you saying. "A homogeneous compound should be, well, homogeneous." And yes, it is – chemically. But there's a difference between raw chemistry and thermodynamics.So why does a homogeneous mixture (like your distilled water) create strata? Well, it's the same concept as the thermocline in the ocean – it comes down to temperature. See, excited molecules move faster (pressure and other things held equal) than slower ones. And as a molecule cools or loses that thermal energy, it slows down. Each "layer" of molecules forms an insulator between the one on either side – absorbing heat from the faster ones but losing it to the slower ones in an effort to create equilibrium.
As molecules slow down, they move out of the way of the faster ones in the stream – more towards the edges of the container. Here, they can serve as lubrication and insulation – they create a smoother surface, and they prevent the rapid heat loss of the inner layers. This property is very important to understanding a waterblock, because it explains the...
Boundary Layer
A specific part of the laminar flow model is the boundary layer. The boundary layer is the portion of your fluid molecules that get stuck on the rough surface of the container. Yes, you read that right – they get stuck. This happens because the surface of your container (the waterblock or tube) is not truly smooth – it's filled with microscopic crevasses and fissures. It also has a lot to do with temperature – the two are very inter-related.So, let's start with the physical issue – the holes. The slower the molecule, the more "outside" it's forced in the fluid's flow. These low energy molecules are easily forced down into the microscopic holes, until they are all filled. Molecules will continue to "stick" until the surface is smooth, creating the next "layer" in the flow. That way, that next layer can flow unimpeded – it doesn't have to deal with the holes, the surface-tension forces created at the edge of a foreign substance or the incredibly rapid change of temperature.

The boundary layer, represented here as a mesh by Rensselaer Polytechnic, is the outermost "skin" of the onion, where
molecules of fluid get stuck together and create a smooth insulating layer for laminar flow.
The problem is, this boundary is actually an insulator, bringing us to the temperature portion. It's the same molecule of water, stuck there permanently (relatively, not really) – it does not get to be cooled off at the radiator. And since it is blocking access to the actual molecules of copper, it's preventing those other layers of water from absorbing as much heat. Though water is a better thermal conductor than air by a longshot, it's also a lot worse than copper – by orders of magnitude. So for every water to water connection instead of water to copper, you're losing very precious heat transfer.
One would think that as these boundary molecules heat up, they will get enough energy to bounce free of their captivity. And this would be true, except for the pressure with which the water moves through the pipe to begin with. Molecules do get "unstuck" and others take their place, but the process is too slow to count on – thermally, it's easiest to assume that (much like electron states being in shells) a portion of molecules are frozen in place, regardless of the eventual turnover.
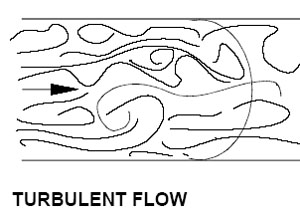
Turbulent flow is the opposite of laminar,
and is chaotic enough to destroy boundary layers..
Beating the layers – Turbulence
The opposite of laminar flow is turbulent flow, and there's good reason for that. When molecules are impeded so as to be unable to stay in one path, they have enough force to break through the layers, regardless of their current temperature.Turbulence in our case is factor of pressure vs. obstacles – being pushed too hard to go in a straight line. In a waterblock, we would accomplish this by the use of some type of "shower head" (for lack of a better word) over the input – something to break the water up and force it to destroy the laminar flow model. Sharp changes in direction will also have this effect, though not to the same extent – hence the "S" patterns frequently found in blocks.
This turbulence is chaotic enough to destroy the boundary layer, which is formed based on holes accessible from the flow's formerly uniform direction. Why do we care? Because for the areas that we can get enough turbulence in, we get the maximum cooling potential – radiating outward from that spot, the potential lessens until the boundary layer reforms as flow moves toward laminar again.
Putting it all together
So, now we know a lot more about the physics behind waterblocks. The block itself should be nothing larger than is required for the internals to work, which should contain lots of surface area. The block is going to be heated from the centre outward, so it's best if most of the surface area is over that spot.In order to make the best use of that surface area, we're going to need the water to flow there first and hardest – that gives it the best opportunity to break up the boundary layer, while providing the "coldest" water (remember, outside of having a measurement right there, temps will show to be uniform through a loop as it reaches equilibrium). Because there's no insulator blocking the copper and the water is at its lowest temperature, it will be able to remove the most heat from the block.
Finally, we need the water to exit the block – but only after it's absorbed every bit of heat that it can pick up along the way. So we should place the exit in a far corner: a longer path inside the block ensures that the water molecule contacts as much surface as possible. However, we should try to reinstate laminar flow and keep obstruction (and hence, pressure drop) to the necessary minimum... so, it helps to make the outside edges that lead to the exit out of the block smooth again
If you'll notice, I've not said much about what the block is topped with – that's because, by and large, it doesn't matter. Tops are connected to the bottoms of blocks with an O-ring in between, so as to prevent leakage. If it isn't, it had better be welded tightly or it should not be in your shopping basket. Because of that, tops don't really affect cooling – they can't draw heat from the block base. So, put whatever you like on it! Polycarbonate, copper, aluminium... if you use two different metals, just keep in mind that corrosion is a factor that you will need to address.
And there we have it – a pretty darn good description of a top-quality waterblock!

MSI MPG Velox 100R Chassis Review
October 14 2021 | 15:04








Want to comment? Please log in.